22 minutes
Encryption-as-a-Service Write-Up
📃 Challenge Description
I built a service that you can use to encrypt your most secret data. It is super secure because the keys never leave the server and are deleted after use!
I love 70s crypto, but now there are cloud services, that crack DES keys for you.
Someone told me that, if I used some non-standard S-box values he gave me, attackers would not be able to use cracking services to get the keys. But after I changed the S-box values he somehow stole my secret flag!
I’m sure he does not own an expensive FPGA cluster, so what is going on?!?
🔎 Research
We are given a single python file, which will run on the server.
The server will generate a random key, receive a plaintext, and encrypt it with the random key using DES in ECB mode. Then it will encrypt the flag with the same key using DES in CBC mode, and sends the encrypted plaintext and encrypted flag back to us.
As the description says, 3 custom SBoxes are used in the DES encryption. I started to analyze the custom SBoxes with differential cryptanalysis.
First, we create our differential tables for the given SBoxes. The main logic is shown below. We simply iterate over all $4096$ possible input value pairs $(x, x^*)$ and count how often the differential of the input pair $x’ = x \oplus x^*$ gives a differential output $y’ = y \oplus y^* = S(x) \oplus S(x^*)$.
def create_diff_table(sbox_number, sbox):
diff_table = DifferentialTable.create(sbox_number + 1)
if diff_table.loaded_from_file:
return diff_table
for x1 in range(64):
for x2 in range(64):
x_diff = u8(diff(x1, x2))
y_diff = u8(diff(sbox[x1], sbox[x2]))
diff_table.add_input_pair_for_output_diff((x1, x2), x_diff, y_diff)
return diff_table
We further save these tables to a file, so we do not have to recalculate when using it again.
📝 Vulnerability Description
So let’s investigate the custom SBox differential tables.
While looking at the tables, i noticed some highly non-uniform distribution in each of the tables.
For $S_3$, if the input differential is $x’ = 0x8$, the output differential of $S_3$ is $y’ = 0x2$ with probability $3/4$.

For $S_4$, if the input differential is $x’ = 0x4$, the output differential of $S_4$ is $y’ = 0x2$ with probability $3/4$.
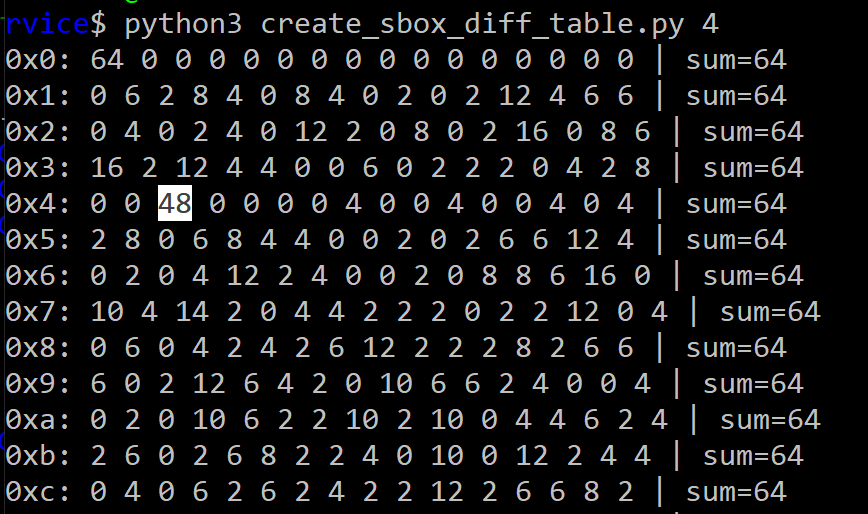
For $S_8$, if the input differential $x’ = 0x8$, the output differential of $S_8$ is $y’ = 0x2$ with probability $3/4$.
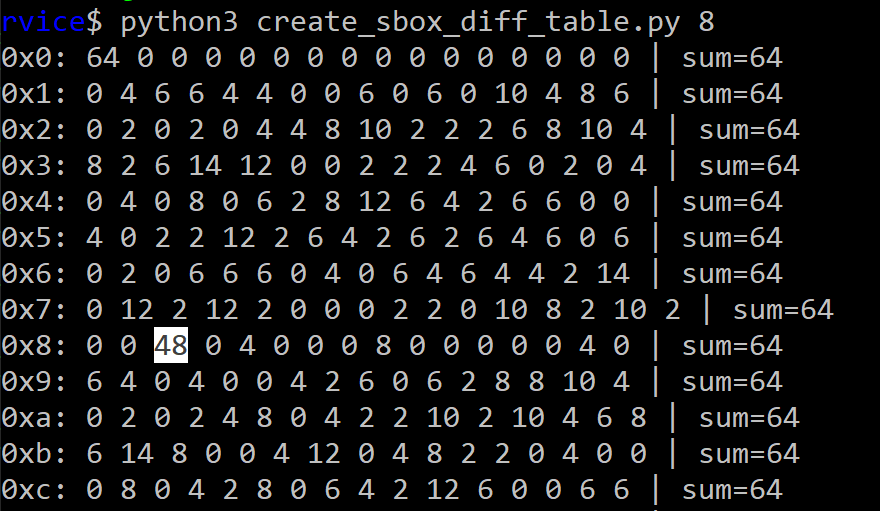
The non-uniform distribution SBoxes are most likely vulnerable to differential cryptanalysis. So lets see what we can do.
🧠 Exploit Development
To exploit the weak SBoxes, we need to find a characteristic. One special kind of characteristic is called an iterative Characteristic. An iterative Characteristic results in the same output as its input, and thus can be chained together. One example for an iterative Characteristic is shown below.
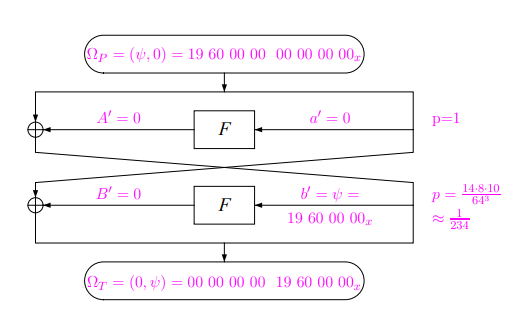
A DES iterative Characteristic
Any amount of rounds that are multiple of 2 results in the differential output $ \Omega_T = (\text{00 00 00 00}, \text{19 60 00 00}) $.
The $f$ function look something like this:
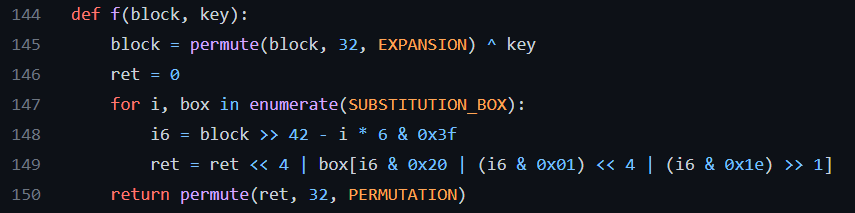
To get the differential input $x’ = 0x8$ for the custom SBoxes $S_3$ and $S_8$, we have to inverse the Expansion Permutation. The Expansion is defined as follows:
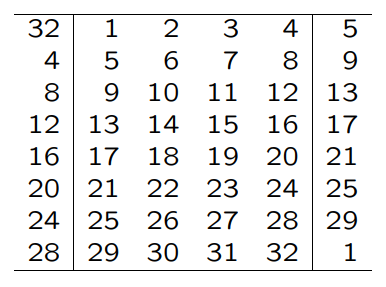
Note, that the Expansion Permutation is linear:
$$ E(X) \oplus E(X^*) = E(X \oplus X^*) = E(X’) $$
To inverse the Expansion i wrote a small script:
from pwn import *
import des.core
def inverse_expansion(sbox_number, expected_output):
expected_output = expected_output & 0xf
important_bit_positions = des.core.EXPANSION[
(sbox_number * 6) : (sbox_number * 6) + 6
]
input_bits = [0 for i in range(32)] # 32bit array
bitarray = bits(expected_output)[2:] # x_diff_of_highest has only 6 bits
for bit_position, bit in zip(important_bit_positions, bitarray):
input_bits[bit_position] = bit
input_bits = u32(unbits(input_bits), endian="big")
return input_bits
For $S_3$ and $S_8$ , we want the expected output to be $x’ = 0x8$, for $S_4$ we want the expected output to be $x’ = 0x4$.
Running this code gives following values:
$S_3: E((\text{00400000})_{16}) \rightarrow S_{3Input} = 0x8$
$S_4: E((\text{00020000})_{16}) \rightarrow S_{4Input} = 0x4$
$S_8: E((\text{00000004})_{16}) \rightarrow S_{8Input} = 0x8$
Note that even if we merge these Expansion input values, they do not disturb each other, because the all have the 2 middle bits set and thus are only used once in the Expansion permutation.
$E((\text{00420004})_{16}) \rightarrow S_{3Input} = 0x8 ; S_{4Input} = 0x4; S_{8Input} = 0x8$
Now we can start to find a characteristic using these values.
I found a 3Round iterative Characteristic with the input differential $\Omega_P = (\text{00 00 00 00}, \text{00 42 00 04})$ and output differential $\Omega_T = (\text{00420004}, \text{00420004})$.
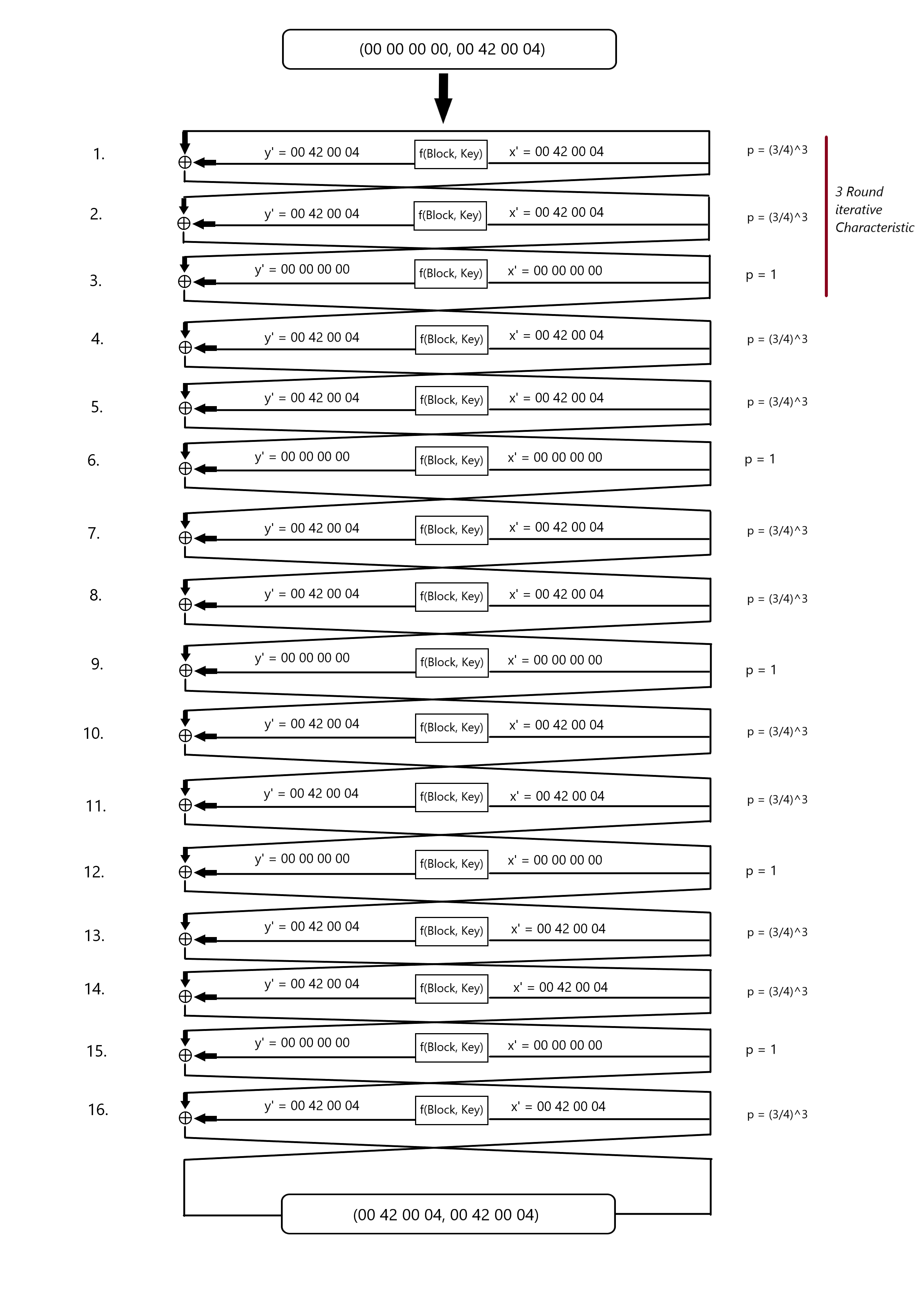
The Probability for a single iteration of this Characteristic is $(\frac{3}{4})^6$ and for all 16 Rounds $(\frac{3}{4})^{3*11}$.
This is not very likely, but as the chosen plaintext is encrypted using ECB Mode, we can send many thousand differential pairs and increase the probability of the characteristic.
The script exploit.py creates 800000 plaintext differential pairs $(P, P*)$, so that the differential $P’ = (\text{00420004})_{16}$
Next, it will receive all encrypted differential pairs $(T, T*)$, inverse the initial Permutation and the last block halves swap of the DES Algorithm, and checks if the Characteristic has occurred, meaning that the differential output $T’ = (\text{0042000400420004})_{16}$.
If that’s the case, we know the differential outputs of $S_3$, $S_4$ and $S_8$. The script will calculate the expanded input pair $(S_E, S_E*)$ to each SBox and their differential $S_E’$. Note that each SBox input is
$$ S_I = S_E \oplus SK. $$
$S_E$ here means the corresponding SBox bits of the expanded permutation of the current block and $S_I$ the actual input to the SBox. Note also that,
$$ S_E’ = (S_E \oplus S_E^*) = (S_I \oplus SK) \oplus (S_I^* \oplus SK) = (S_I \oplus S_I^*) = S_I' $$
We retrieve the possible input pairs $(x, x*)$ from the differential table for the differential input $x’ = S_I’ = S_E’$ which lead to the differential output $y’$ for the Characteristic (for this Characteristic 0x2).
Using each value of the actual input pair $(S_I, S_I^*)$ we can calculate a set of possible subkey bits.
$$ SK = S_I \oplus S_E $$
$$ SK = S_I^* \oplus S_E^* $$
We save those two possible subkey values in a set and calculate the intersection of all of these sets corresponding to a single SBox. After the intersection, the set contains all possible values for a specific subkey.
With this technique we reduced the keybits of the first derived subkey from 56 to 38. The rest I decided to simply brute force. The descrack.cpp file does that.
After we found the key, we can decrypt the encrypted flag.
🔐 Exploit Program
exploit.py:
import binascii
import des.core
from pwn import *
from create_sbox_diff_table import *
from inverse_permutation import *
def split_block(b):
return b >> 32, b & 0xFFFFFFFF
def swap_block_halves(b):
return (b & 0xFFFFFFFF) << 32 | (b >> 32) & 0xFFFFFFFF
class DESCharacteristic:
def __init__(
self, sbox_number, input_block, output_block, sbox_output_diff
) -> None:
self.SBOX_NUMBER = sbox_number - 1 # starts at 0
self.INPUT = input_block
self.OUTPUT = output_block
self.SBOX_OUTPUT_DIFF = sbox_output_diff
self.DIFF_TABLE = create_diff_table(
self.SBOX_NUMBER, SBox(des.core.SUBSTITUTION_BOX[self.SBOX_NUMBER])
)
class InputPair:
def __init__(self, pair, characteristics) -> None:
self.PAIR = pair
self.CHARACTERISTICS = characteristics
@classmethod
def create_for_characteristic(cls, characteristic, *extra_characteristics):
# create input pair, so that x' = x1 ^ x2 = characteristic.INPUT
x1 = random.getrandbits(64)
x2 = x1 ^ characteristic.INPUT
input_pair = (
des.core.permute(x1, 64, des.core.INVERSE_PERMUTATION),
des.core.permute(x2, 64, des.core.INVERSE_PERMUTATION),
)
characteristics = [characteristic] + list(extra_characteristics)
return cls(input_pair, characteristics)
counter = 0
def get_keybyte_set_for_characteristic(
characteristic, diff_table, input_pair, output_pair
):
global counter
o1 = des.core.permute(
u64(output_pair[0], endian="big"),
64,
des.core.INITIAL_PERMUTATION,
)
o2 = des.core.permute(
u64(output_pair[1], endian="big"),
64,
des.core.INITIAL_PERMUTATION,
)
output_pair = (swap_block_halves(o1), swap_block_halves(o2)) # reverse last flip
output_diff = output_pair[0] ^ output_pair[1]
# print("Output Diff: ", hex(output_diff))
if output_pair[0] ^ output_pair[1] != characteristic.OUTPUT:
# Characteristic has not occurred
return {i for i in range(0x3F)}
# Characteristic has occurred, continue
counter+=1
# we know differential outputs of S_3,S_4 and S_8 = characteristic.SBOX_OUTPUT_DIFF, because the characteristic occurred (we can see this on the output pairs)
input_pair_1 = des.core.permute(input_pair[0], 64, des.core.INITIAL_PERMUTATION)
input_pair_2 = des.core.permute(input_pair[1], 64, des.core.INITIAL_PERMUTATION)
input_block_1 = split_block(input_pair_1)[1]
input_block_2 = split_block(input_pair_2)[1]
expanded_input_block_1 = des.core.permute(input_block_1, 32, des.core.EXPANSION)
expanded_input_block_2 = des.core.permute(input_block_2, 32, des.core.EXPANSION)
expanded_sbox_input_1 = (
expanded_input_block_1 >> 42 - characteristic.SBOX_NUMBER * 6 & 0x3F
)
expanded_sbox_input_2 = (
expanded_input_block_2 >> 42 - characteristic.SBOX_NUMBER * 6 & 0x3F
)
input_diff = u8(diff(expanded_sbox_input_1, expanded_sbox_input_2))
input_pairs = diff_table.get_input_pairs_for_output_diff(
input_diff, characteristic.SBOX_OUTPUT_DIFF
)
keybyte_set = set()
for expanded_sbox_input in (expanded_sbox_input_1, expanded_sbox_input_2):
for x1, x2 in input_pairs:
keybyte_set.add(x1 ^ expanded_sbox_input)
keybyte_set.add(x2 ^ expanded_sbox_input)
return keybyte_set
# Probability for 3Round Iterative Characteristic: (3/4)^3
# Probability for Iterative Characteristic to occur in 16Round DES: ((3/4)^(11*3))
# -> approx. 1/((3/4)^(11*3)) = 13273 differential pairs are needed.
s3_characteristic = DESCharacteristic(3, 0x00420004, 0x0042000400420004, 0x2)
s4_characteristic = DESCharacteristic(4, 0x00420004, 0x0042000400420004, 0x2)
s8_characteristic = DESCharacteristic(8, 0x00420004, 0x0042000400420004, 0x2)
input_pairs = list()
for _ in range(800000):
input_pairs.append(InputPair.create_for_characteristic(s3_characteristic, s4_characteristic, s8_characteristic))
# convert input_pairs to hex input
input_hex = b""
for input_pair in input_pairs:
input_hex += b"".join(
[binascii.hexlify(p64(value, endian="big")) for value in input_pair.PAIR]
)
input_hex += b"4141414142424242" # test value to test master key
p = process("./main.py")
# p = remote(
# "f091172e8befbcbbea2b35c0-encryption-as-a-service.challenge.master.cscg.live", 31337, ssl=True
# )
p.recvuntil(b"(hex): ")
p.sendline(input_hex)
print(str(p.recvline(keepends=False).decode()))
ct = binascii.unhexlify(p.recvline(keepends=False)[12:])
# print(bytearray(ct).hex())
ENCRYPTED_FLAG = binascii.unhexlify(p.recvline(keepends=False)[6:])
print("Encrypted Flag: ", bytearray(ENCRYPTED_FLAG).hex())
TEST_ENCRYPTED = ct[(len(input_pairs) * 16) : (len(input_pairs) * 16) + 8]
print("Test Encrypted: ", bytearray(TEST_ENCRYPTED).hex())
keybytes = [{i for i in range(0x3F+1)} for _ in range(8)]
for idx, input_pair in enumerate(input_pairs):
output_pair = ct[idx * 16 : (idx * 16) + 8], ct[(idx * 16) + 8 : (idx * 16) + 16]
for characteristic in input_pair.CHARACTERISTICS:
keybyte_set = get_keybyte_set_for_characteristic(
characteristic,
characteristic.DIFF_TABLE,
input_pair.PAIR,
output_pair,
)
keybytes[characteristic.SBOX_NUMBER].intersection_update(keybyte_set)
for idx, key in enumerate(keybytes):
print(f"Possible Keybits for S{idx+1}_K: ", str(key))
print("Characteristic occurred:", str(counter))
des.c:
/*
* Data Encryption Standard
* An approach to DES algorithm
*
* By: Daniel Huertas Gonzalez
* Email: huertas.dani@gmail.com
* Version: 0.1
*
* Based on the document FIPS PUB 46-3
*/
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#define LB32_MASK 0x00000001
#define LB64_MASK 0x0000000000000001
#define L64_MASK 0x00000000ffffffff
#define H64_MASK 0xffffffff00000000
/* Initial Permutation Table */
static char IP[] = {
58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6,
64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7};
/* Inverse Initial Permutation Table */
static char PI[] = {
40, 8, 48, 16, 56, 24, 64, 32,
39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30,
37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28,
35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25};
/*Expansion table */
static char E[] = {
32, 1, 2, 3, 4, 5,
4, 5, 6, 7, 8, 9,
8, 9, 10, 11, 12, 13,
12, 13, 14, 15, 16, 17,
16, 17, 18, 19, 20, 21,
20, 21, 22, 23, 24, 25,
24, 25, 26, 27, 28, 29,
28, 29, 30, 31, 32, 1};
/* Post S-Box permutation */
static char P[] = {
16, 7, 20, 21,
29, 12, 28, 17,
1, 15, 23, 26,
5, 18, 31, 10,
2, 8, 24, 14,
32, 27, 3, 9,
19, 13, 30, 6,
22, 11, 4, 25};
/* The S-Box tables */
static char S[8][64] = {{/* S1 */
14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7,
0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8,
4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0,
15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13},
{/* S2 */
15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10,
3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5,
0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15,
13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9},
{/* S3 */
// 10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8,
// 13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1,
// 13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7,
// 1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12},
5, 8, 13, 6, 7, 2, 15, 4, 11, 14, 0, 3, 9, 12, 10, 1,
3, 2, 15, 11, 1, 0, 12, 9, 13, 6, 7, 8, 14, 4, 5, 10,
0, 15, 7, 14, 2, 9, 5, 12, 4, 11, 10, 1, 6, 13, 8, 3,
12, 6, 1, 5, 14, 4, 3, 7, 0, 8, 15, 10, 2, 11, 13, 9},
{/* S4 */
// 7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15,
// 13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9,
// 10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4,
// 3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14},
4, 13, 6, 10, 12, 0, 14, 2, 15, 9, 8, 11, 5, 1, 7, 3,
7, 9, 10, 11, 0, 14, 2, 12, 13, 4, 15, 6, 3, 5, 1, 8,
10, 5, 0, 7, 6, 9, 4, 11, 8, 14, 2, 12, 1, 13, 3, 15,
5, 3, 7, 1, 10, 6, 8, 4, 9, 15, 11, 0, 2, 14, 13, 12},
{/* S5 */
2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9,
14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6,
4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14,
11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3},
{/* S6 */
12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11,
10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8,
9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6,
4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13},
{/* S7 */
4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1,
13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6,
1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2,
6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12},
{/* S8 */
// 13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7,
// 1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2,
// 7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8,
// 2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11}
8, 0, 15, 7, 12, 2, 13, 5, 3, 10, 11, 6, 1, 14, 9, 4,
11, 12, 3, 5, 9, 14, 1, 13, 7, 0, 4, 8, 15, 2, 6, 10,
7, 9, 10, 0, 5, 11, 8, 14, 1, 4, 13, 2, 3, 6, 15, 12,
9, 4, 8, 3, 1, 6, 10, 11, 0, 14, 5, 13, 2, 12, 7, 15}};
/* Permuted Choice 1 Table */
static char PC1[] = {
57, 49, 41, 33, 25, 17, 9,
1, 58, 50, 42, 34, 26, 18,
10, 2, 59, 51, 43, 35, 27,
19, 11, 3, 60, 52, 44, 36,
63, 55, 47, 39, 31, 23, 15,
7, 62, 54, 46, 38, 30, 22,
14, 6, 61, 53, 45, 37, 29,
21, 13, 5, 28, 20, 12, 4};
/* Permuted Choice 2 Table */
static char PC2[] = {
14, 17, 11, 24, 1, 5,
3, 28, 15, 6, 21, 10,
23, 19, 12, 4, 26, 8,
16, 7, 27, 20, 13, 2,
41, 52, 31, 37, 47, 55,
30, 40, 51, 45, 33, 48,
44, 49, 39, 56, 34, 53,
46, 42, 50, 36, 29, 32};
/* Iteration Shift Array */
static char iteration_shift[] = {
/* 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 */
1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1};
/*
* The DES function
* input: 64 bit message after INITIAL_PERMUTATION
* key: 64 bit key after PC1 for encryption/decryption
* mode: 'e' = encryption; 'd' = decryption
*/
uint64_t des(uint64_t input, uint64_t key, char mode)
{
int i, j;
/* 8 bits */
char row, column;
/* 28 bits */
uint32_t C = 0;
uint32_t D = 0;
/* 32 bits */
uint32_t L = 0;
uint32_t R = 0;
uint32_t s_output = 0;
uint32_t f_function_res = 0;
uint32_t temp = 0;
/* 48 bits */
uint64_t sub_key[16] = {0};
uint64_t s_input = 0;
/* 56 bits */
uint64_t permuted_choice_1 = 0;
uint64_t permuted_choice_2 = 0;
/* 64 bits */
uint64_t init_perm_res = 0;
uint64_t inv_init_perm_res = 0;
uint64_t pre_output = 0;
/* initial permutation */
// for (i = 0; i < 64; i++)
// {
// init_perm_res <<= 1;
// init_perm_res |= (input >> (64 - IP[i])) & LB64_MASK;
// }
// L = (uint32_t)(init_perm_res >> 32) & L64_MASK;
// R = (uint32_t)init_perm_res & L64_MASK;
// We skip IP for performance reasons and provide input as if it were after IP
L = (uint32_t)(input >> 32) & L64_MASK;
R = (uint32_t)input & L64_MASK;
/* initial key schedule calculation */
// for (i = 0; i < 56; i++)
// {
// permuted_choice_1 <<= 1;
// permuted_choice_1 |= (key >> (64 - PC1[i])) & LB64_MASK;
// }
// C = (uint32_t)((permuted_choice_1 >> 28) & 0x000000000fffffff);
// D = (uint32_t)(permuted_choice_1 & 0x000000000fffffff);
// We skip PC1 for performance reasons and provide key as if it were after PC1
C = (uint32_t)((key >> 28) & 0x000000000fffffff);
D = (uint32_t)(key & 0x000000000fffffff);
/* Calculation of the 16 keys */
for (i = 0; i < 16; i++)
{
/* key schedule */
// shifting Ci and Di
for (j = 0; j < iteration_shift[i]; j++)
{
C = 0x0fffffff & (C << 1) | 0x00000001 & (C >> 27);
D = 0x0fffffff & (D << 1) | 0x00000001 & (D >> 27);
}
permuted_choice_2 = 0;
permuted_choice_2 = (((uint64_t)C) << 28) | (uint64_t)D;
sub_key[i] = 0;
for (j = 0; j < 48; j++)
{
sub_key[i] <<= 1;
sub_key[i] |= (permuted_choice_2 >> (56 - PC2[j])) & LB64_MASK;
}
}
for (i = 0; i < 16; i++)
{
/* f(R,k) function */
s_input = 0;
for (j = 0; j < 48; j++)
{
s_input <<= 1;
s_input |= (uint64_t)((R >> (32 - E[j])) & LB32_MASK);
}
/*
* Encryption/Decryption
* XORing expanded Ri with Ki
*/
if (mode == 'd')
{
// decryption
s_input = s_input ^ sub_key[15 - i];
}
else
{
// encryption
s_input = s_input ^ sub_key[i];
}
/* S-Box Tables */
for (j = 0; j < 8; j++)
{
// 00 00 RCCC CR00 00 00 00 00 00 s_input
// 00 00 1000 0100 00 00 00 00 00 row mask
// 00 00 0111 1000 00 00 00 00 00 column mask
row = (char)((s_input & (0x0000840000000000 >> 6 * j)) >> 42 - 6 * j);
row = (row >> 4) | row & 0x01;
column = (char)((s_input & (0x0000780000000000 >> 6 * j)) >> 43 - 6 * j);
s_output <<= 4;
s_output |= (uint32_t)(S[j][16 * row + column] & 0x0f);
}
f_function_res = 0;
for (j = 0; j < 32; j++)
{
f_function_res <<= 1;
f_function_res |= (s_output >> (32 - P[j])) & LB32_MASK;
}
temp = R;
R = L ^ f_function_res;
L = temp;
}
pre_output = (((uint64_t)R) << 32) | (uint64_t)L;
/* inverse initial permutation */
for (i = 0; i < 64; i++)
{
inv_init_perm_res <<= 1;
inv_init_perm_res |= (pre_output >> (64 - PI[i])) & LB64_MASK;
}
return inv_init_perm_res;
}
descrack.c:
extern "C"
{
#include "des.c"
}
#include <iostream>
#include <bitset>
#include <string>
static char INVERSE_PERMUTED_CHOICE1[] = {7, 15, 23, 55, 51, 43, 35, 0, 6, 14, 22, 54, 50, 42, 34, 0, 5, 13, 21, 53, 49, 41, 33, 0, 4, 12, 20, 52, 48, 40, 32, 0, 3, 11, 19, 27, 47, 39, 31, 0, 2, 10, 18, 26, 46, 38, 30, 0, 1, 9, 17, 25, 45, 37, 29, 0, 0, 8, 16, 24, 44, 36, 28};
static char INVERSE_PERMUTED_CHOICE2[] = {4, 23, 6, 15, 5, 9, 19, 17, 0, 11, 2, 14, 22, 0, 8, 18, 1, 0, 13, 21, 10, 0, 12, 3, 0, 16, 20, 7, 46, 30, 26, 47, 34, 40, 0, 45, 27, 0, 38, 31, 24, 43, 0, 36, 33, 42, 28, 35, 37, 44, 32, 25, 41, 0, 29, 39};
static char PERMUTED_CHOICE2_LOST_BITS[] = {8, 17, 21, 24, 34, 37, 42, 53};
// IP(0x4141414142424242) = 0xff00000f000000f0
static uint64_t TEST_INPUT_AFTER_INITIAL_PERMUTATION = 0xff00000f000000f0;
static uint64_t TEST_ENCRYPTED = 0xff92e096e515b920;
// ENC_FLAG = dd8cf7033377602cfdb3e6bdf41a79f90a863761fab1543cb3418207679948701511f6dbeb4fb292179d053bfc561b8de3f0bdd456c8e8b8d0aebe78f620f4905bb035bb6b04d6a89e30c384f1e08747eb32a652d4ac6ee9c62d66d830155820e4a49028211374cb
template <size_t input_bits, size_t output_bits>
inline std::bitset<output_bits> permute_inverse(uint64_t input, char *mapper)
{
std::bitset<input_bits> input_bitset{input};
std::bitset<output_bits> output_bitset{0x0};
for (size_t i{0}; i < output_bits; ++i)
{
output_bitset[output_bits - 1 - i] = input_bitset[input_bits - 1 - mapper[i]];
}
return output_bitset;
}
inline void brute_with_key(uint64_t key)
{
auto next_key = permute_inverse<48, 56>(key, INVERSE_PERMUTED_CHOICE2);
uint32_t C;
uint32_t D;
for (uint16_t i = {0}; i <= 0xff; ++i)
{
// Fill in PERMUTED_CHOICE2_LOST_BITS
next_key[55 - 8] = (i & 0x1);
next_key[55 - 17] = ((i >> 1) & 0x1);
next_key[55 - 21] = ((i >> 2) & 0x1);
next_key[55 - 24] = ((i >> 3) & 0x1);
next_key[55 - 34] = ((i >> 4) & 0x1);
next_key[55 - 37] = ((i >> 5) & 0x1);
next_key[55 - 42] = ((i >> 6) & 0x1);
next_key[55 - 53] = ((i >> 7) & 0x1);
// try to decrypt with next_key
uint64_t temp_key = next_key.to_ullong();
C = (uint32_t)((temp_key >> 28) & 0x000000000fffffff);
D = (uint32_t)(temp_key & 0x000000000fffffff);
// rotate each half right by 1bit
C = (C & 0x1) << 27 | (C >> 1) & 0x0FFFFFFF;
D = (D & 0x1) << 27 | (D >> 1) & 0x0FFFFFFF;
temp_key = ((uint64_t)C << 28) | (D & 0x0FFFFFFF);
if (des(TEST_INPUT_AFTER_INITIAL_PERMUTATION, temp_key, 'e') == TEST_ENCRYPTED)
{
std::cout << "Found Key (after PC1): " << std::hex << temp_key << std::endl;
temp_key = permute_inverse<56, 64>(temp_key, INVERSE_PERMUTED_CHOICE1).to_ullong();
std::cout << "Found Key (before PC1): " << std::hex << temp_key << std::endl;
exit(0);
}
}
}
int main(int argc, const char *argv[])
{
uint8_t start = 0;
int end = 63;
if (argc == 3)
{
start = std::stoi(argv[1]);
end = std::stoi(argv[2]);
if (start < 0 || start > 63 || end > 63 || end < 0)
{
std::cout << "Invalid Start or End! Should be in range [0,63]" << std::endl;
exit(0);
}
}
std::cout << "Bruting Keys starting with SK_1=" << (int)start << " till SK_1=" << (int)end << std::endl;
// approx. 100'000 encryptions per second
uint8_t SK_1[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63};
uint8_t SK_2[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63};
uint8_t SK_3[] = {20, 28};
uint8_t SK_4[] = {3, 7};
uint8_t SK_5[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63};
uint8_t SK_6[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63};
uint8_t SK_7[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63};
uint8_t SK_8[] = {55};
for (; end >= start; --end)
{
uint8_t k1 = SK_1[end];
for (auto k2 : SK_2)
{
for (auto k3 : SK_3)
{
for (auto k4 : SK_4)
{
for (auto k5 : SK_5)
{
for (auto k6 : SK_6)
{
for (auto k7 : SK_7)
{
for (auto k8 : SK_8)
{
uint64_t key = static_cast<uint64_t>(k1 & 0x3f) << 42 | static_cast<uint64_t>(k2 & 0x3f) << 36 | static_cast<uint64_t>(k3 & 0x3f) << 30 | static_cast<uint64_t>(k4 & 0x3f) << 24 | static_cast<uint64_t>(k5 & 0x3f) << 18 | static_cast<uint64_t>(k6 & 0x3f) << 12 | static_cast<uint64_t>(k7 & 0x3f) << 6 | (k8 & 0x3f);
brute_with_key(key);
}
}
}
}
}
}
}
std::cout << "SK_1 (" << end - start << " left)\n";
}
std::cout << "Search Exhausted" << std::endl;
}
💥 Run Exploit
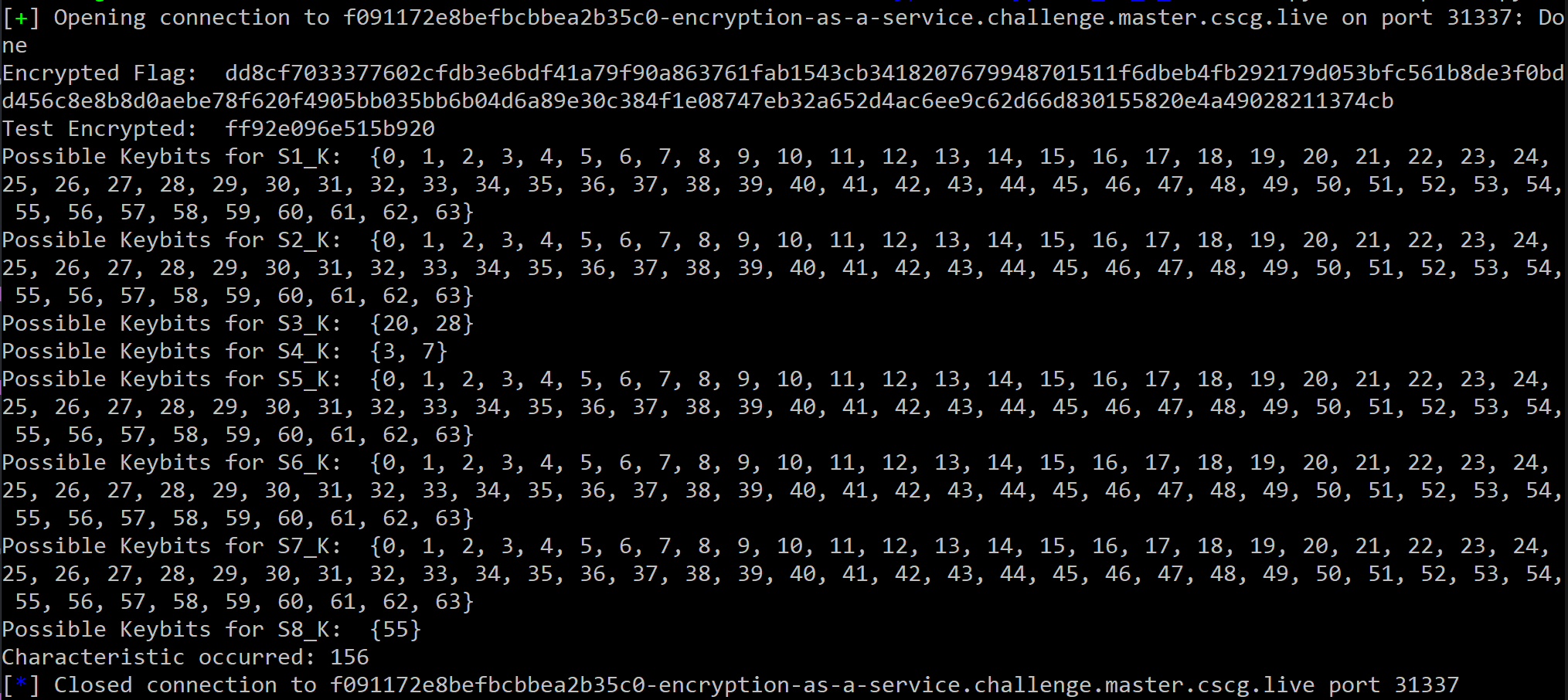

FLAG: CSCG{wait_trusting_crypto_constants_from_random_internet_strangers_is_not_a_good_idea???}
🛡️ Possible Prevention
As the flag already says, simply trusting and copy and pasting crypto constants from random strangers is not a good idea. Generally, use the Cryptographic methods that are popular and known to be secure, as these are mostly the ones which are being the most analyzed algorithms. That being said, one could use Triple-DES or just stick with AES to secure this encryption service. In Addition, don’t use the ECB Mode for Block ciphers. Use others like CBC, OFB, or with Authenticated Encryption use Modes like GCM or SIV.
🗄️ Summary / Difficulties
This was a really enjoyable challenge, as it was the first time for me looking into the field of Cryptanalysis and especially differential cryptanalysis.
Note, that the presented solution is not the only one and requires a brute force of 38 bits. Other characteristics could potentially reduce the keybits further.
Nothing left to say. Great Challenge ;)