Casino Write-Up

📃 Challenge Description

Making decisions is hard. Even for smart people like Diffie or Hellman. Maybe you can still win the lottery somehow 🤷.

🔎 Research

We are given one python script with which we can interact.

from flag import FLAG
import random

rng = random.SystemRandom()

# Secure group from RFC 3526
prime = int("""
FFFFFFFF FFFFFFFF C90FDAA2 2168C234 C4C6628B 80DC1CD1
29024E08 8A67CC74 020BBEA6 3B139B22 514A0879 8E3404DD
EF9519B3 CD3A431B 302B0A6D F25F1437 4FE1356D 6D51C245
E485B576 625E7EC6 F44C42E9 A637ED6B 0BFF5CB6 F406B7ED
EE386BFB 5A899FA5 AE9F2411 7C4B1FE6 49286651 ECE45B3D
C2007CB8 A163BF05 98DA4836 1C55D39A 69163FA8 FD24CF5F
83655D23 DCA3AD96 1C62F356 208552BB 9ED52907 7096966D
670C354E 4ABC9804 F1746C08 CA18217C 32905E46 2E36CE3B
E39E772C 180E8603 9B2783A2 EC07A28F B5C55DF0 6F4C52C9
DE2BCBF6 95581718 3995497C EA956AE5 15D22618 98FA0510
15728E5A 8AACAA68 FFFFFFFF FFFFFFFF""".replace('\n', '').replace(' ', ''), 
16)

generator = 11

def play():
    challenge = rng.randint(0, 1)

    a, b, z = rng.randint(1, prime-1), rng.randint(1, prime-1), rng.randint(1, prime-1)

    A, B, C, Z = pow(generator, a, prime), pow(generator, b, prime), pow(generator, a*b, prime), pow(generator, z, prime)

    print(f"""Guess the random bit I have coosen!
Commitment: {A}, {B}, {C if challenge == 1 else Z}""")

    guess = int(input("> ").strip())

    if guess == challenge:
        print(f"""Correct! My challenge was {challenge}
Proof: {a}, {b}""")
        return 1
    else:
        print(f"""Wrong! My challenge was {challenge}
Proof: {a}, {b}""")
        return -1

def main():
    balance = 100

    print(f"""Welcome to the first casino with fully provable randomness using cryptographically hard problems!
It uses the Decisional Diffie-Hellman Problem to provide a commitment, which can be verified by the player after the answer has been given.
Your balance is {balance} €.
Aquire 200 € to get one of our premium flags
    """)

    while True:
        balance += play()

        if balance <= 0:
            exit(0)

        if balance >= 200:
            print(FLAG)
            exit(0)

        print(f"Your current balance is {balance} €\n")

if __name__ == '__main__':
    main()

The Goal in this challenge consists of reaching at least 200€ by repeatedly answering the decisional Diffie-Hellman Problem with more correct answers than incorrect ones. This means that we must have a vulnerability which allows us to know the answer with more evidence than just pure luck (more than 50 percent probability of correctness).

The Decisional Diffie-Hellman Problem (DDH) states that for three numbers $A = g^a \pmod p$ , $B = g^b \pmod p$ and $C = g^c \pmod p$, where $c$ is either randomly and evenly distributed across ${0, …, p-2}$, or $c = ab \pmod p$, in which case $(A,B,C)$ is called a Diffie-Hellman-Triple, it is impossible to decide with only the information of $(A,B,C)$, whether $(A,B,C)$ is a Diffie-Hellman-Triple or not. So the problem is to decide for a given $g^a \pmod p$, $g^b \pmod p$ and $g^c \pmod p$, if $g^c = g^{ab}$.

We can see the DDH being implemented in the play function, where the third commitment value we get is based on the challenge variable either C, in which case the three values form a Diffie-Hellman-Triple, or Z, in which case they form with a very high probability not a Diffie-Hellman-Triple.

Now, lets look at the prime number and generator used in the script. The prime number is copied from RFC 3526, which is shown below:

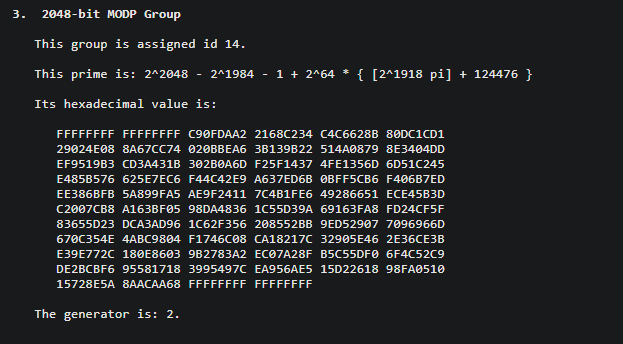
Untitled

The used generator however is 11, which is different from the generator specified in RFC 3526.

📝 Vulnerability Description

The DDH is vulnerable if the generator used is a primitive root. In more detail, if $p$ is a prime number, $g$ a primitive root modulo $p$ and $a,b \in {0, …, p-2}$, then $g^{ab}$ is a quadratic residue modulo $p$, if $g^a$ or $g^b$ is a quadratic residue modulo $p$.

We can show that the generator 11 is in fact a primitive root modulo prime. But first, lets look at what so called Safe Primes are. A Safe Prime number $p$ is a prime number so that $q = (p-1)/2$ is also a prime number. In this case $q$ is called a Sophie Germain prime number. We can show with sage that the prime number prime is in fact a Safe Prime:

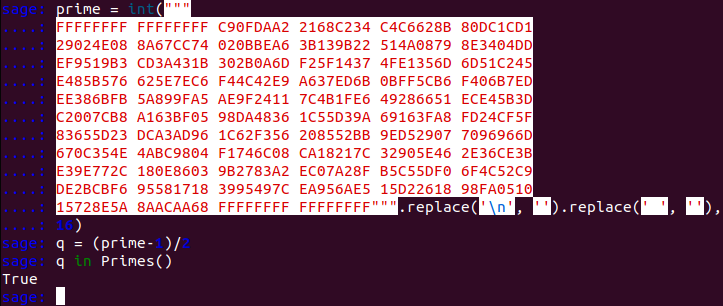
Untitled1

Now, that prime is a Safe Prime there are only two conditions that need to be satisfied for the generator to be a primitive root modulo prime:

$g^2 \neq 1 \pmod p$
$g^{(p-1)/2} \neq 1 \pmod p$

we can verify both conditions with sage:

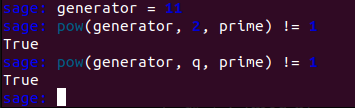
Untitled2

Lastly, with the first theorem and knowledge that generator is a primitive root modulo prime, we can reliably decide if the third commitment value is C or Z:

if A or B is a quadratic residue modulo prime, the third commitment value is likely to be C if it is also a quadratic residue modulo prime,
else we cannot be sure and default to guess it was Z.

Good To Know: Concluded from euler’s criterion, a number $a$ is a Quadratic Residue modulo an odd prime number $p$ if $a^{(p-1)/2} \equiv 1 \pmod p$.

🔐 Exploit Program

from pwn import *

# Secure group from RFC 3526
prime = int("""
FFFFFFFF FFFFFFFF C90FDAA2 2168C234 C4C6628B 80DC1CD1
29024E08 8A67CC74 020BBEA6 3B139B22 514A0879 8E3404DD
EF9519B3 CD3A431B 302B0A6D F25F1437 4FE1356D 6D51C245
E485B576 625E7EC6 F44C42E9 A637ED6B 0BFF5CB6 F406B7ED
EE386BFB 5A899FA5 AE9F2411 7C4B1FE6 49286651 ECE45B3D
C2007CB8 A163BF05 98DA4836 1C55D39A 69163FA8 FD24CF5F
83655D23 DCA3AD96 1C62F356 208552BB 9ED52907 7096966D
670C354E 4ABC9804 F1746C08 CA18217C 32905E46 2E36CE3B
E39E772C 180E8603 9B2783A2 EC07A28F B5C55DF0 6F4C52C9
DE2BCBF6 95581718 3995497C EA956AE5 15D22618 98FA0510
15728E5A 8AACAA68 FFFFFFFF FFFFFFFF""".replace('\n', '').replace(' ', ''), 
16)
generator = 11 # weak, is primitive root
# (prime-1)/2 in Primes() -> True
# pow(generator, (prime-1)/2, prime) != 1 -> True

host = "795a6de34c7a49907fd35157-casino.challenge.master.cscg.live"
port = 31337
p = remote(host, port, ssl=True)
# p = 2q+1 -> "safe prime"
# q = (p-1)/2 -> "Sophie Germain prime"
q = 16158503035655503650169456963211914124408970620570119556421004875700370853317177111309844708681784673558950868954852095877302936604597514426879493092811076606087706257450887260135117898039118124442123094738793820552964323049705861622713311261096615270459518840262117759562839857935058500529027938825519430923640128988027451784866280763083540669680899770668238279580184158948364536589192294840319835950488601097084323612935515705668214659768096735818266604858538724113994294282684604322648318038625134477752964181375560587048486499034205277179792433291645821068109115539495499724326234131208486017955926253522680545279

def is_quadratic_residue_in_prime(x):
	return pow(x, q, prime) == 1

def play():
	p.recvuntil(b"Commitment: ")
	A = int(p.recvuntil(b",", drop=True).strip().decode())
	B = int(p.recvuntil(b",", drop=True).strip().decode())
	CorZ = int(p.recvuntil(b"\n", drop=True).strip().decode())
	guess = 0
	if is_quadratic_residue_in_prime(A) or is_quadratic_residue_in_prime(B):
		guess = is_quadratic_residue_in_prime(CorZ)
	p.sendlineafter(b"> ", b"1" if guess else b"0")
	return b"Correct!" in p.recvline()

if __name__ == "__main__":
	balance = 100
	while(balance < 200):
		balance += 1 if play() else -1
		print(f"balance: {balance!s}")
	p.recvline()
	print(p.recvline())

💥 Run Exploit

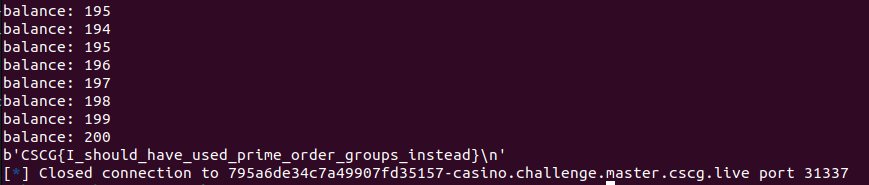
Untitled3

FLAG: CSCG{I_should_have_used_prime_order_groups_instead}

🛡️ Possible Prevention

To prevent this type of attack against the DDH, the generator has to be chosen so that it is not a primitive root modulo the prime number. By using the generator equals 2, as specified in RFC 3526, the second condition for a primitive root is not satisfied anymore:

Untitled4

Thus, we can no longer have a reliable way to choose one answer with more winning chance than 50%.

🗃️ Further References

Quadratic residue

primitive root of a very big prime number (Elgamal DS)

Diffie-Hellman-Schlüsselaustausch

RFC 3526: More Modular Exponential (MODP) Diffie-Hellman groups for Internet Key Exchange (IKE)